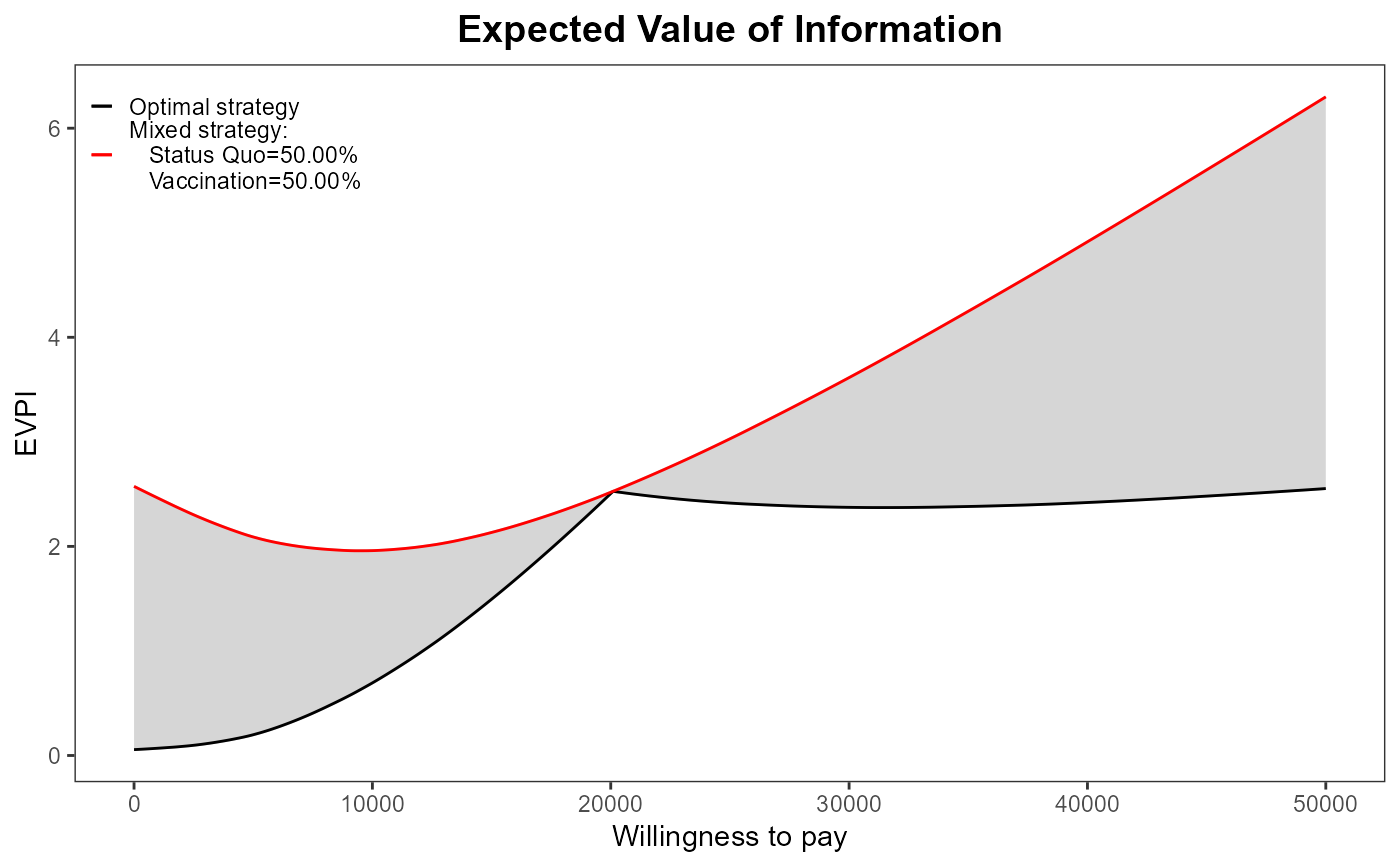
EVI Plot of the Health Economic Analysis For Mixed Analysis

Compares the optimal scenario to the mixed case in terms of the EVPI.

Usage

# S3 method for mixedAn
evi.plot(he, y.limits = NULL, pos = c(0, 1), graph = c("base", "ggplot2"), ...)

Arguments

he: An object of class mixedAn, a subclass of bcea, given as output of the call to the function mixedAn().
y.limits: Range of the y-axis for the graph. The default value is NULL, in which case the maximum range between the optimal and the mixed analysis scenarios is considered.
pos: Parameter to set the position of the legend (only relevant for multiple interventions, ie more than 2 interventions being compared). Can be given in form of a string (bottom|top)(right|left) for base graphics and bottom|top|left|right for ggplot2. It can be a two-elements vector, which specifies the relative position on the x and y axis respectively, or alternatively it can be in form of a logical variable, with FALSE indicating to use the default position and TRUE to place it on the bottom of the plot.
graph: A string used to select the graphical engine to use for plotting. Should (partial-)match the two options "base" or "ggplot2". Default value is "base".
...: Arguments to be passed to methods, such as graphical parameters (see par()).

Value

evi: A ggplot object containing the plot. Returned only if graph="ggplot2".

The function produces a graph showing the difference between the ''optimal'' version of the EVPI (when only the most cost-effective intervention is included in the market) and the mixed strategy one (when more than one intervention is considered in the market).

References

Baio G, Russo P (2009). “A decision-theoretic framework for the application of cost-effectiveness analysis in regulatory processes.” Pharmacoeconomics, 27(8), 5--16. ISSN 20356137, doi:10.1007/bf03320526 .

Baio G, Dawid aP (2011). “Probabilistic sensitivity analysis in health economics.” Stat. Methods Med. Res., 1--20. ISSN 1477-0334, doi:10.1177/0962280211419832 , https://pubmed.ncbi.nlm.nih.gov/21930515/.

Baio G (2013). Bayesian Methods in Health Economics. CRC.

Author

Gianluca Baio, Andrea Berardi

Examples

# See Baio G., Dawid A.P. (2011) for a detailed description of the 
# Bayesian model and economic problem
#
# Load the processed results of the MCMC simulation model
data(Vaccine)

# Runs the health economic evaluation using BCEA
m <- bcea(e=eff, c=cost,    # defines the variables of 
                            #  effectiveness and cost
      ref=2,                # selects the 2nd row of (e,c) 
                            #  as containing the reference intervention
      interventions=treats, # defines the labels to be associated 
                            #  with each intervention
      Kmax=50000,           # maximum value possible for the willingness 
                            #  to pay threshold; implies that k is chosen 
                            #  in a grid from the interval (0,Kmax)
      plot=FALSE            # inhibits graphical output
)

mixedAn(m) <- NULL      # uses the results of the mixed strategy 
                        #  analysis (a "mixedAn" object)
                        # the vector of market shares can be defined 
                        #  externally. If NULL, then each of the T 
                        #  interventions will have 1/T market share
                        # produces the plots
evi.plot(m)


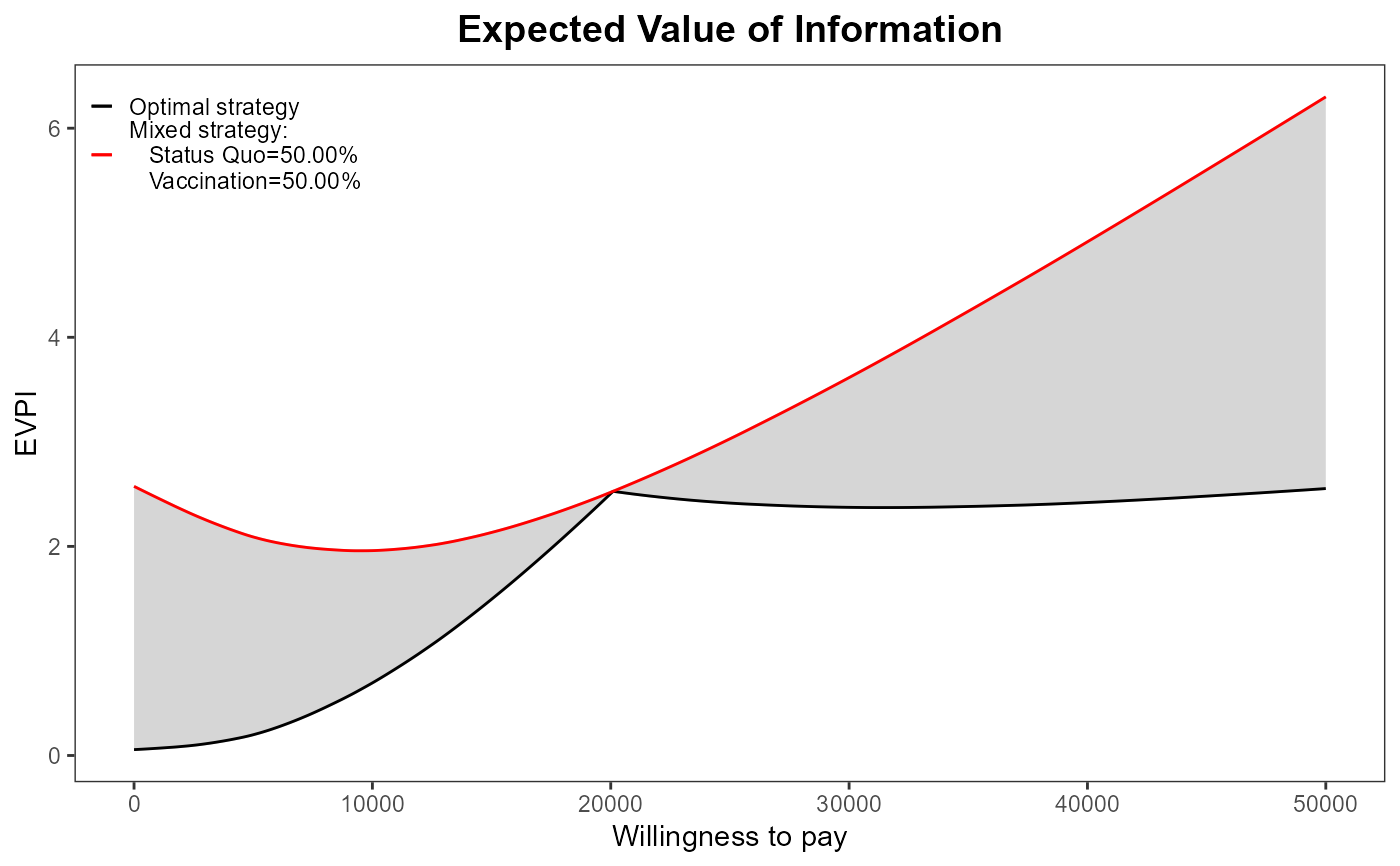evi.plot(m, graph="base")


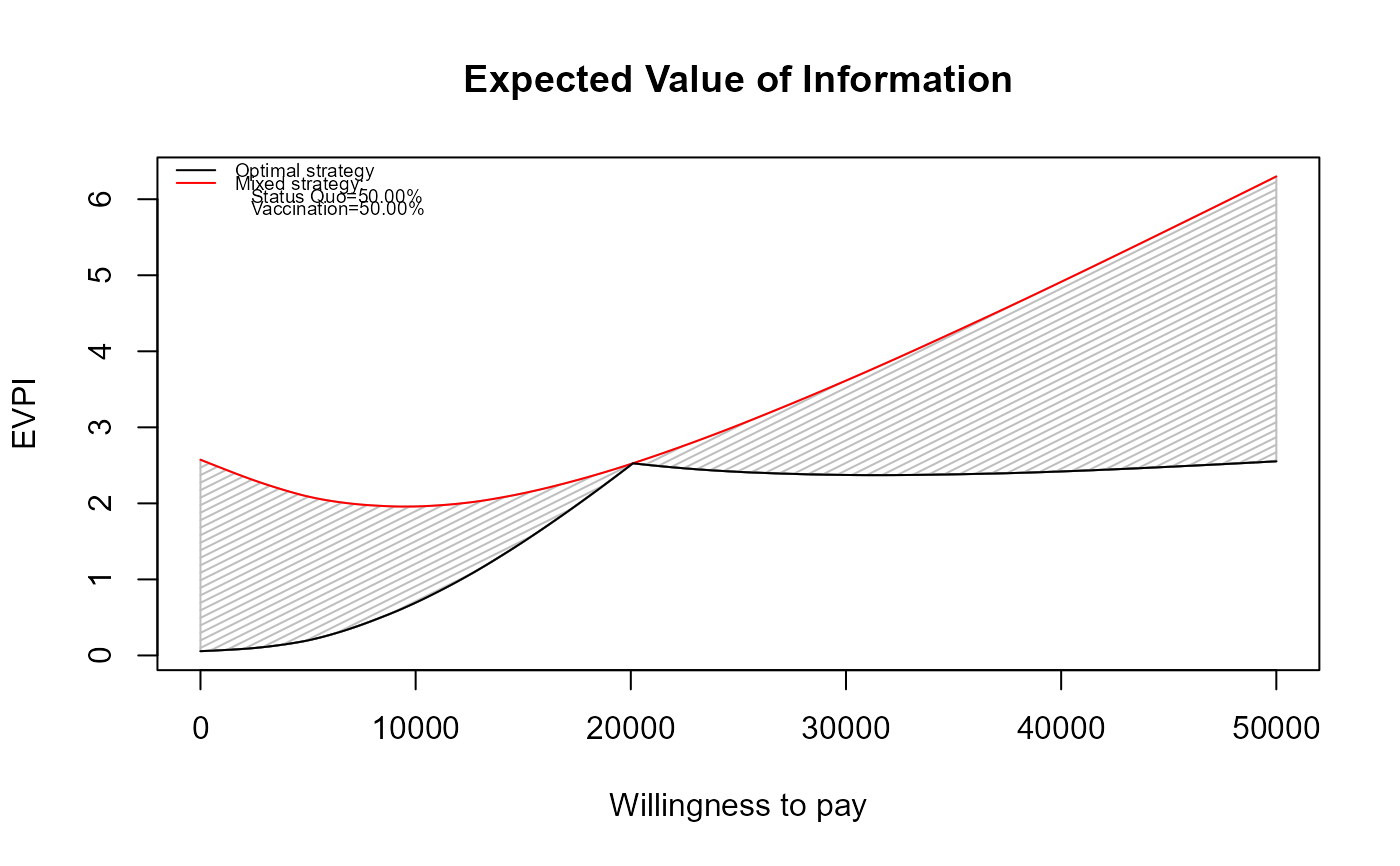# Or with ggplot2
if (require(ggplot2)) {
   evi.plot(m, graph="ggplot2")
}