Introduction
The intention of this vignette is to show how to plot different styles of cost-effectiveness acceptability curves using the BCEA package.
Two interventions only
This is the simplest case, usually an alternative intervention (\(i=1\)) versus status-quo (\(i=0\)).
The plot show the probability that the alternative intervention is cost-effective for each willingness to pay, \(k\),
\[ p(NB_1 \geq NB_0 | k) \mbox{ where } NB_i = ke - c \]
Using the set of \(N\) posterior samples, this is approximated by
\[ \frac{1}{N} \sum_j^N \mathbb{I} (k \Delta e^j - \Delta c^j) \]
R code
To calculate these in BCEA we use the bcea()
function.
data("Vaccine")
he <- bcea(eff, cost)
#> No reference selected. Defaulting to first intervention.
# str(he)
ceac.plot(he)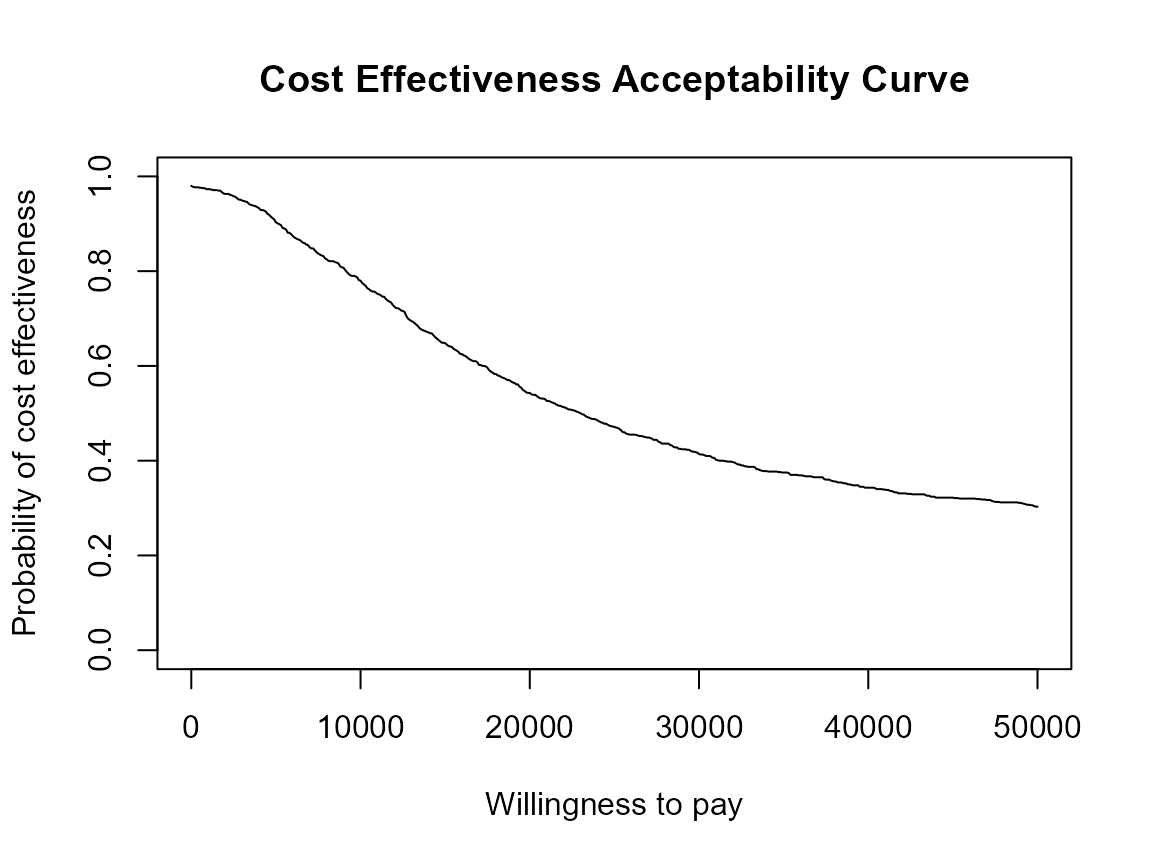
The plot defaults to base R plotting. Type of plot can be set
explicitly using the graph argument.
ceac.plot(he, graph = "base")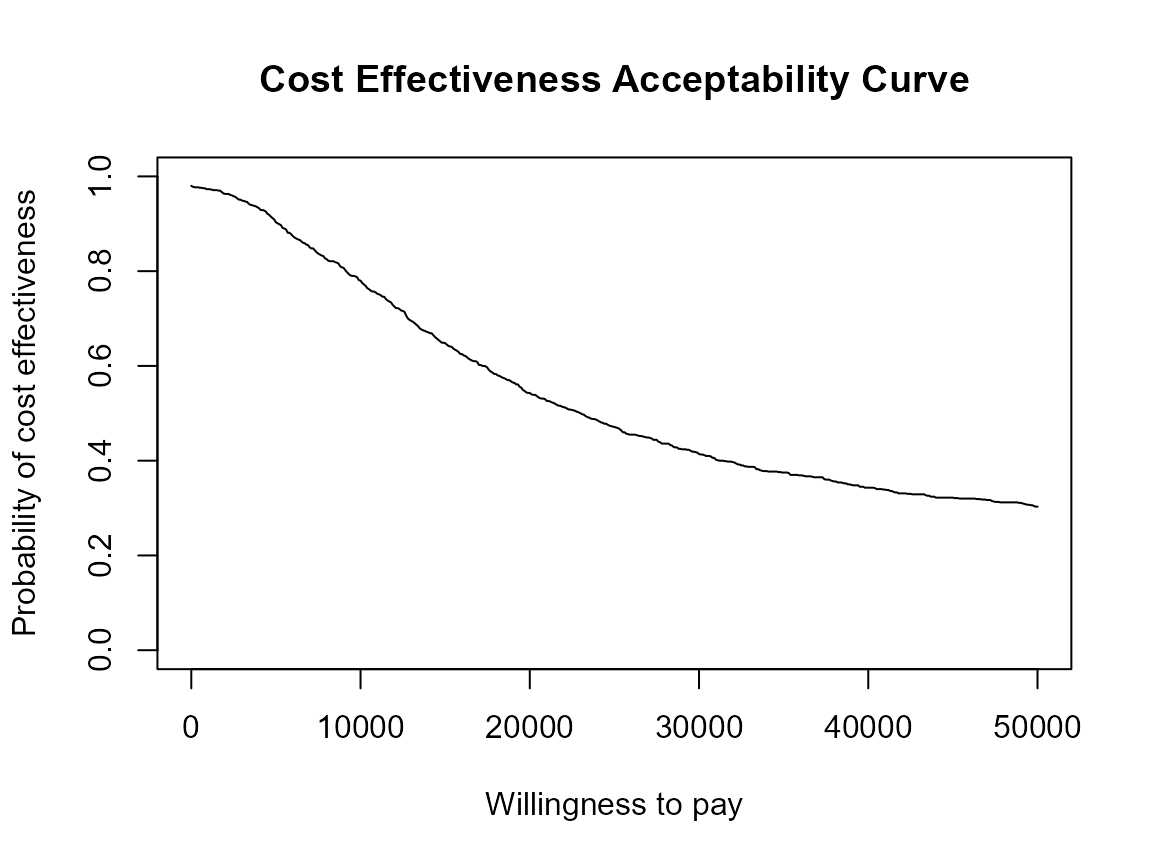
ceac.plot(he, graph = "ggplot2")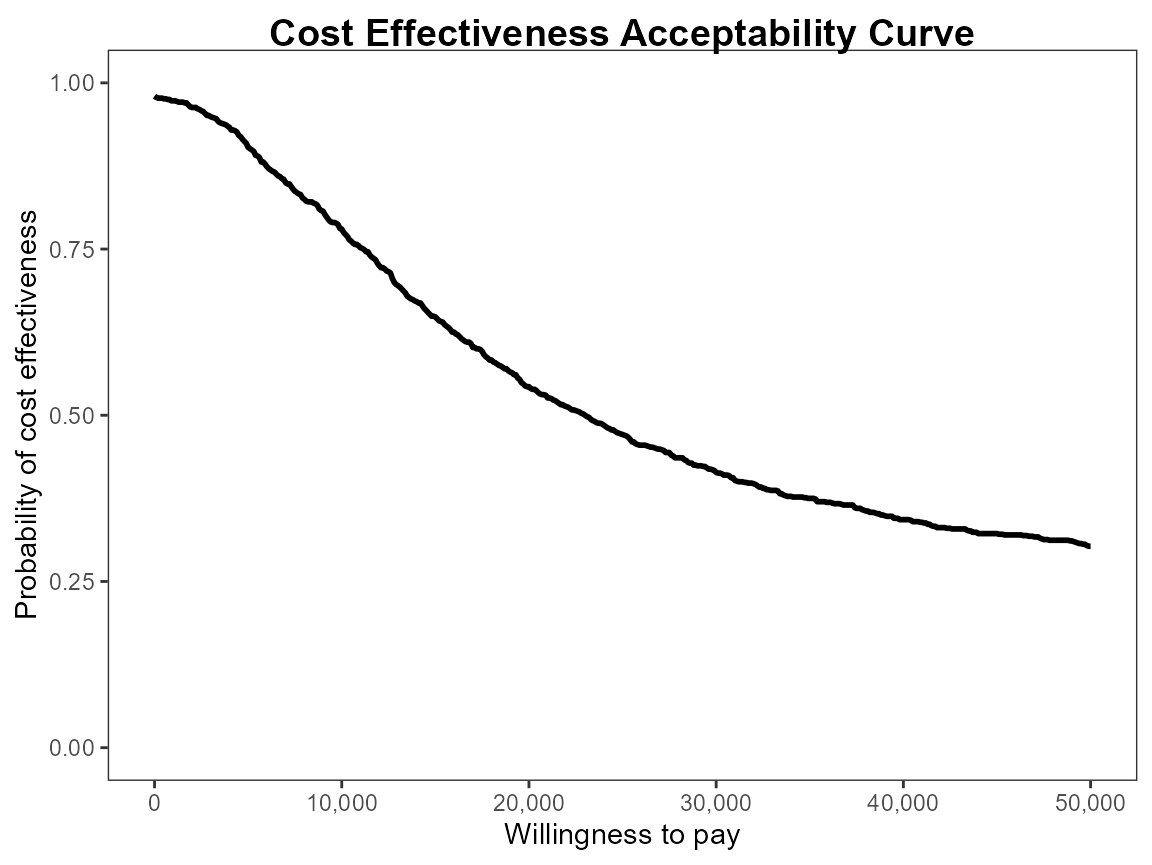
# ceac.plot(he, graph = "plotly")Other plotting arguments can be specified such as title, line colours and theme.
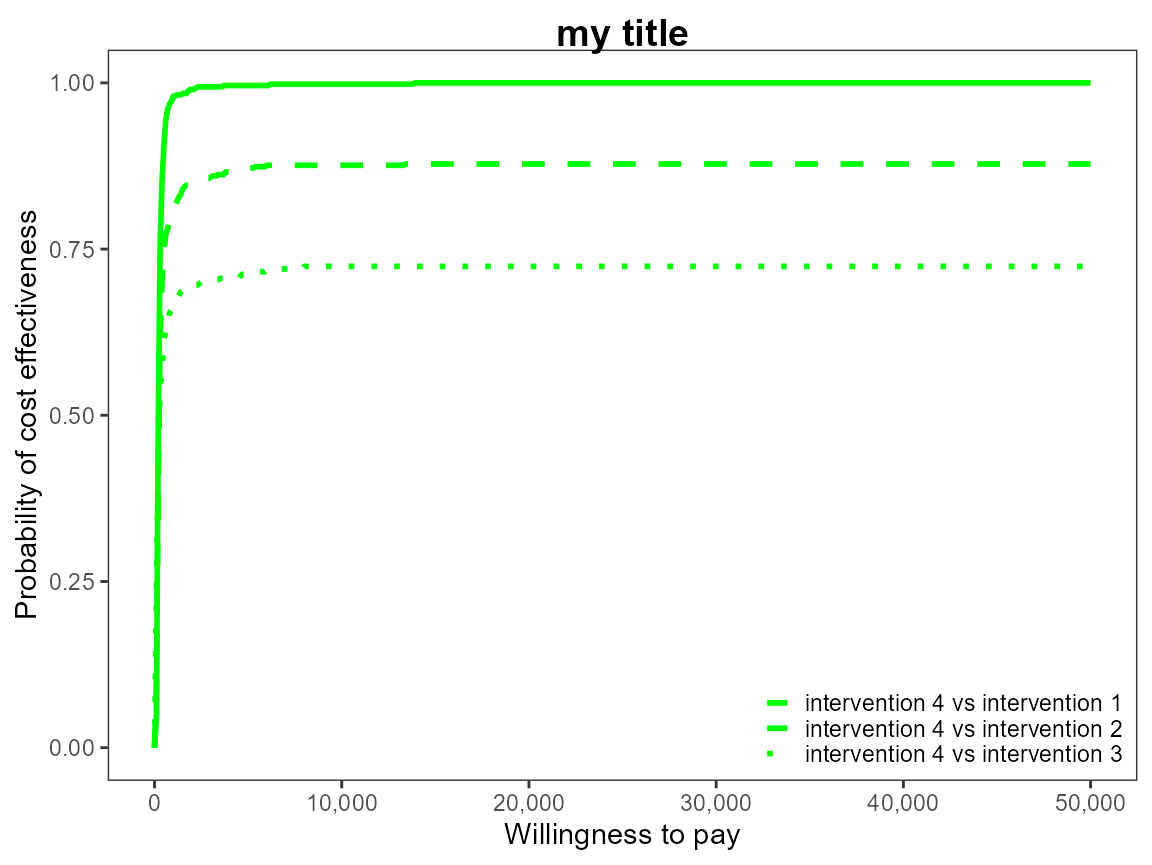
ceac.plot(he,
graph = "ggplot2",
title = "my title",
line = list(color = "green"),
theme = theme_dark())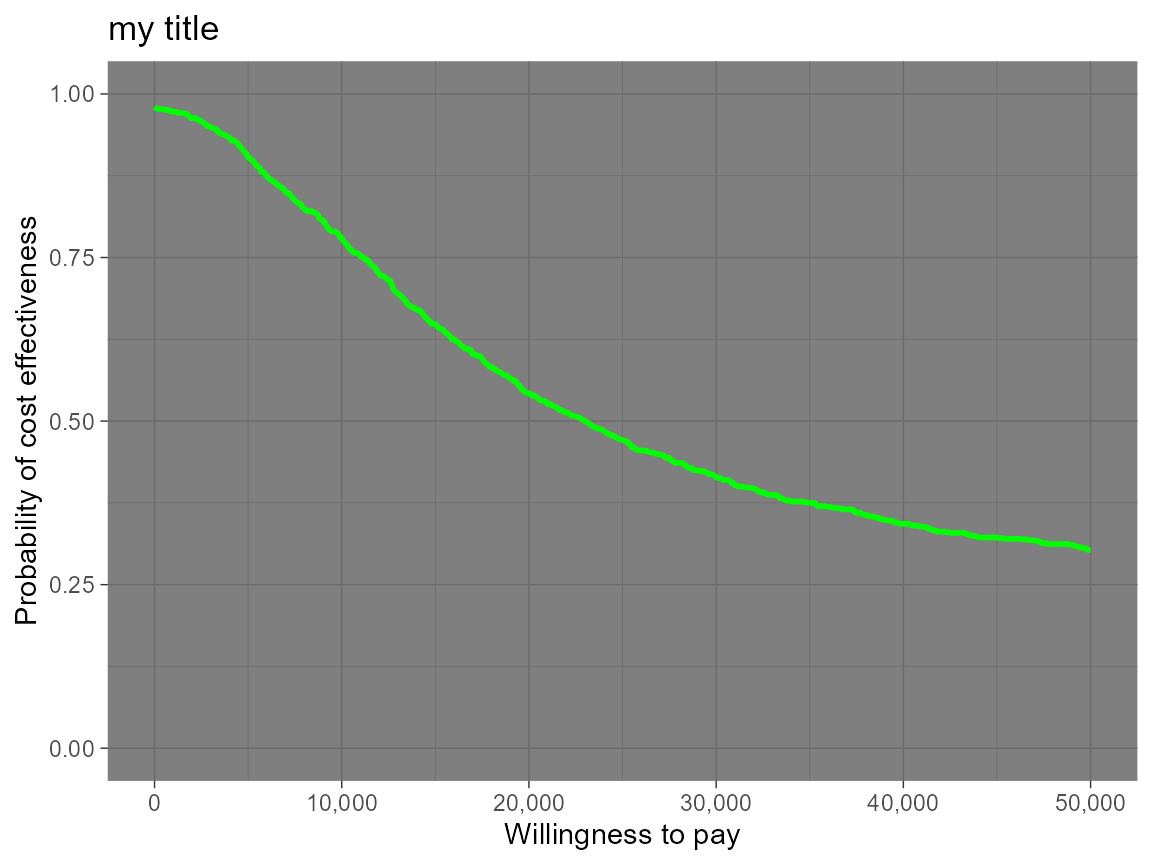
Multiple interventions
This situation is when there are more than two interventions to consider. Incremental values can be obtained either always against a fixed reference intervention, such as status-quo, or for all pair-wise comparisons.
Against a fixed reference intervention
Without loss of generality, if we assume that we are interested in intervention \(i=1\), then we wish to calculate
\[ p(NB_1 \geq NB_s | k) \;\; \exists \; s \in S \]
Using the set of \(N\) posterior samples, this is approximated by
\[ \frac{1}{N} \sum_j^N \mathbb{I} (k \Delta e_{1,s}^j - \Delta c_{1,s}^j) \]
R code
This is the default plot for ceac.plot() so we simply
follow the same steps as above with the new data set.
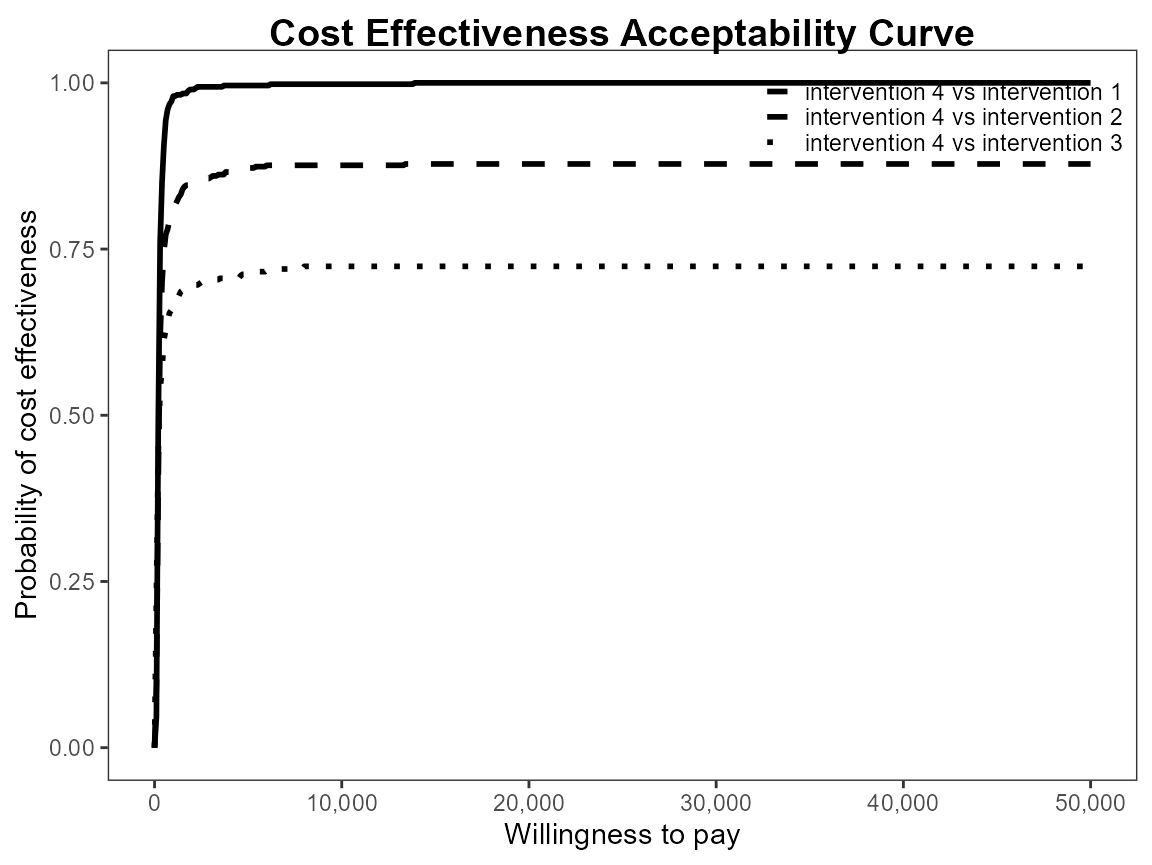
ceac.plot(he)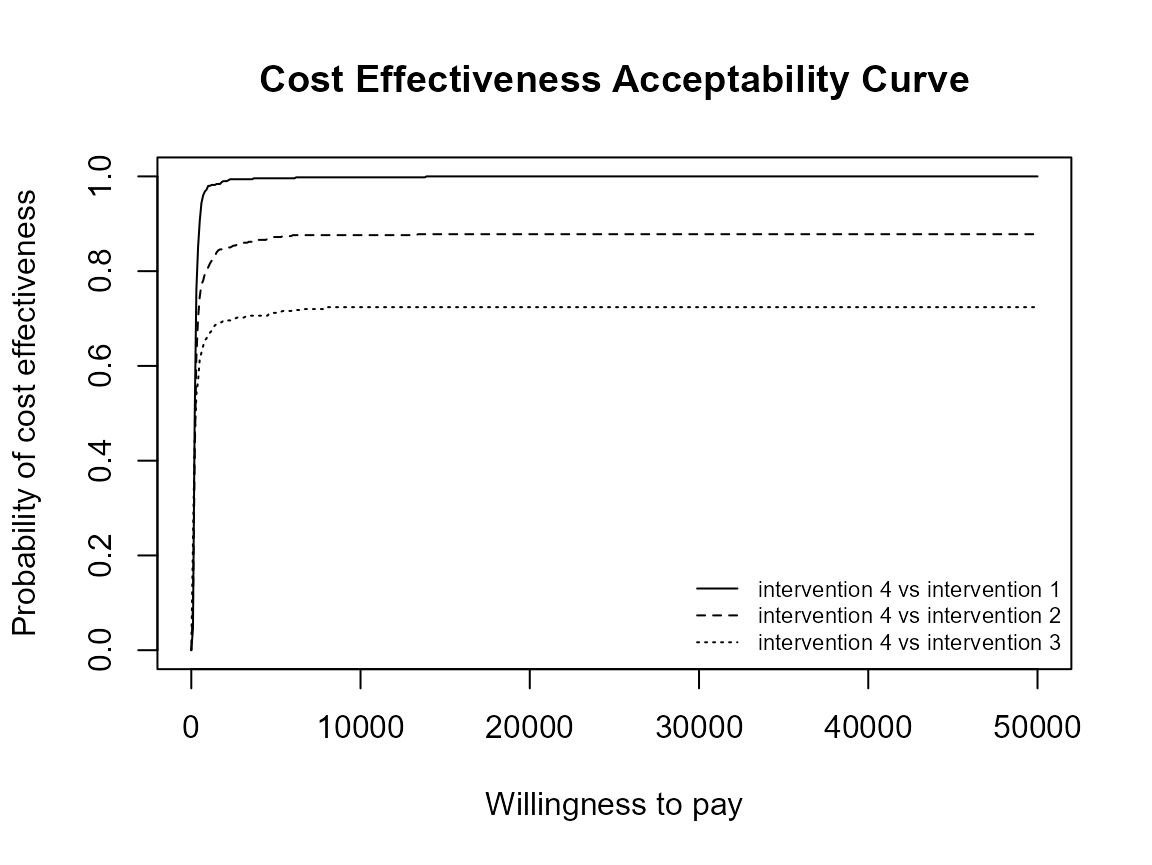
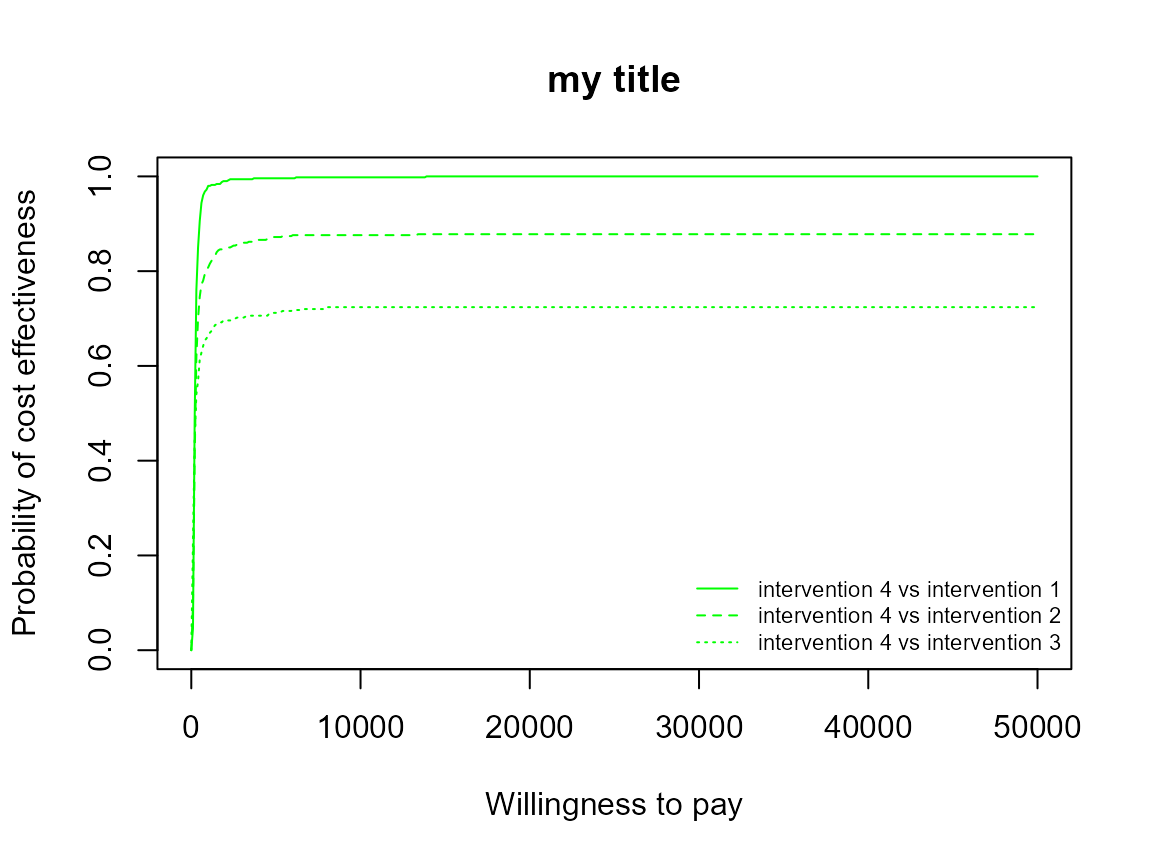
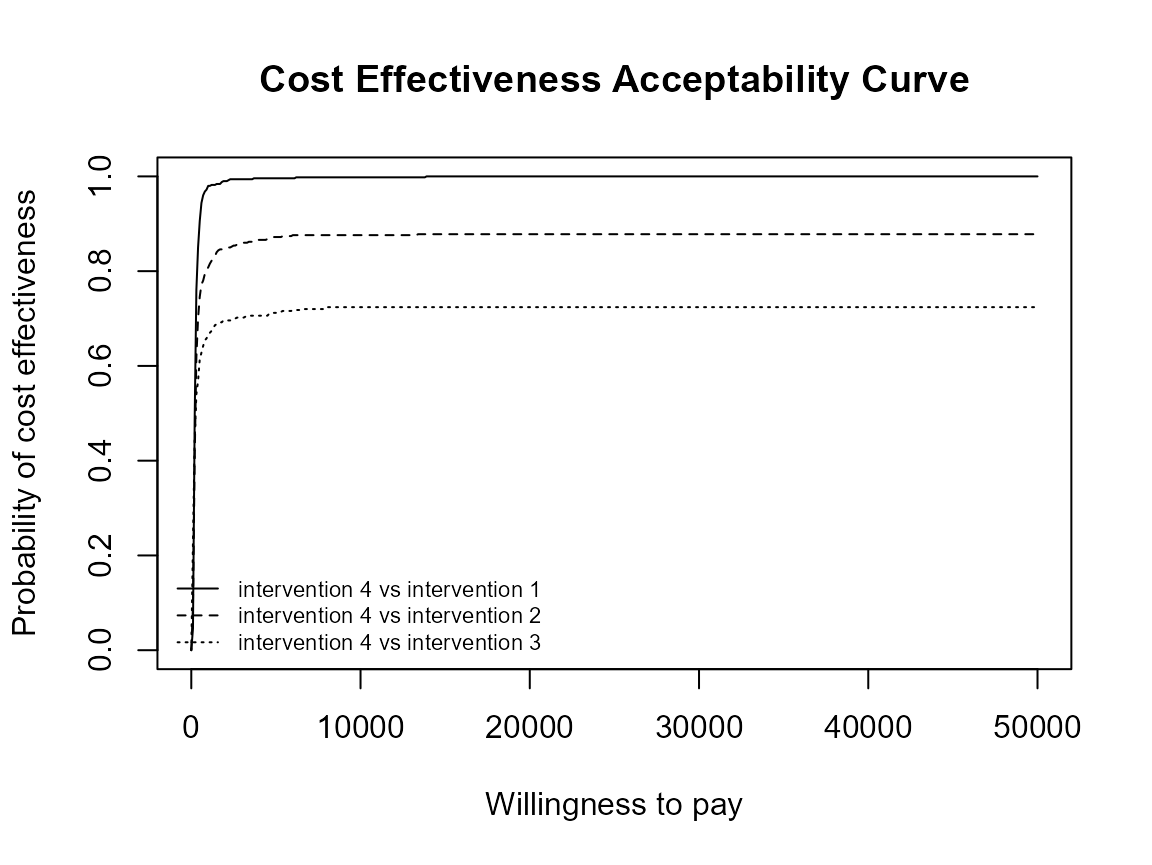
Reposition legend.
ceac.plot(he, pos = FALSE) # bottom right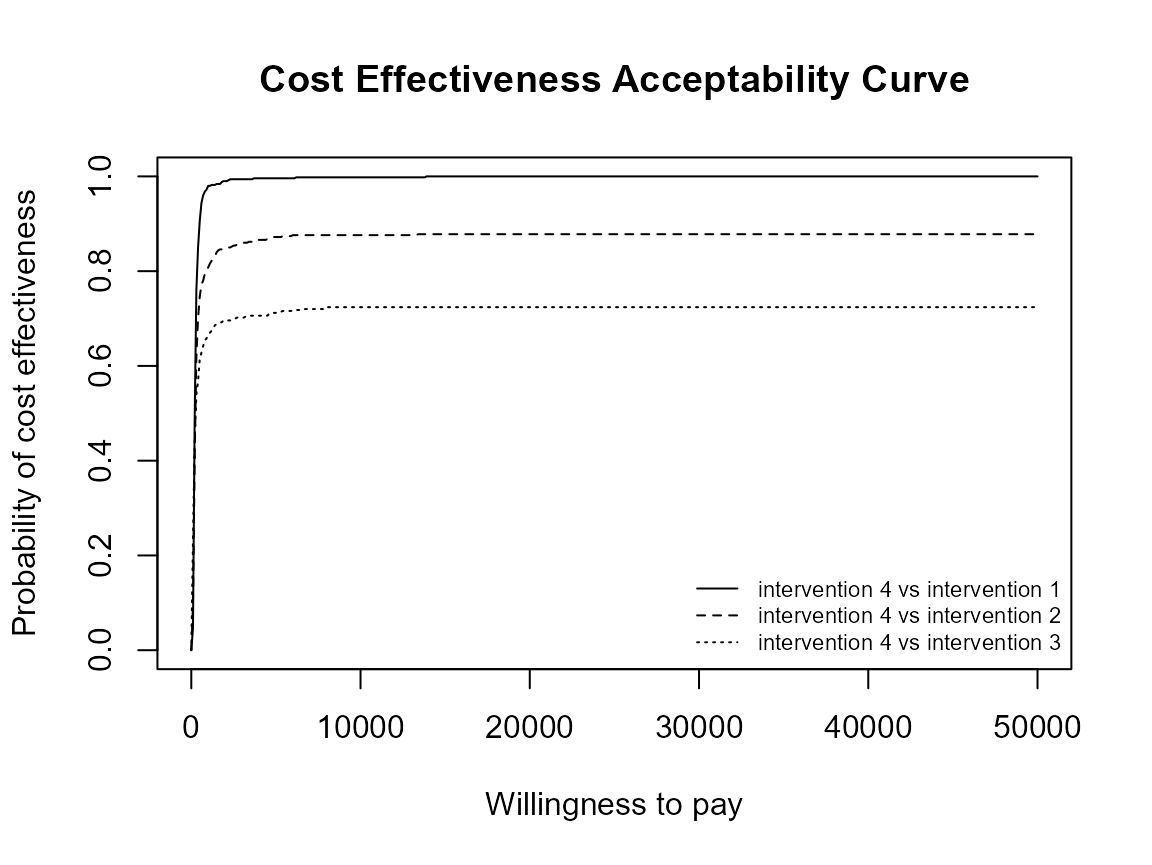
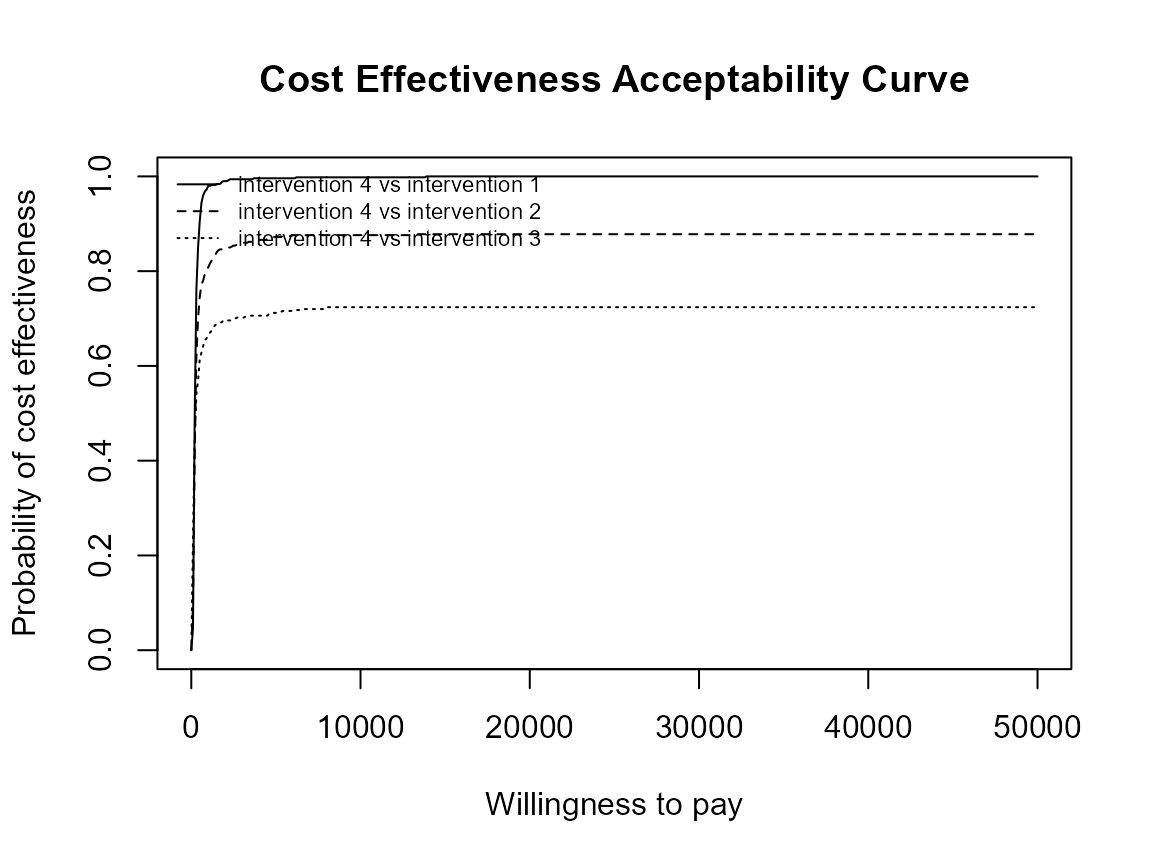
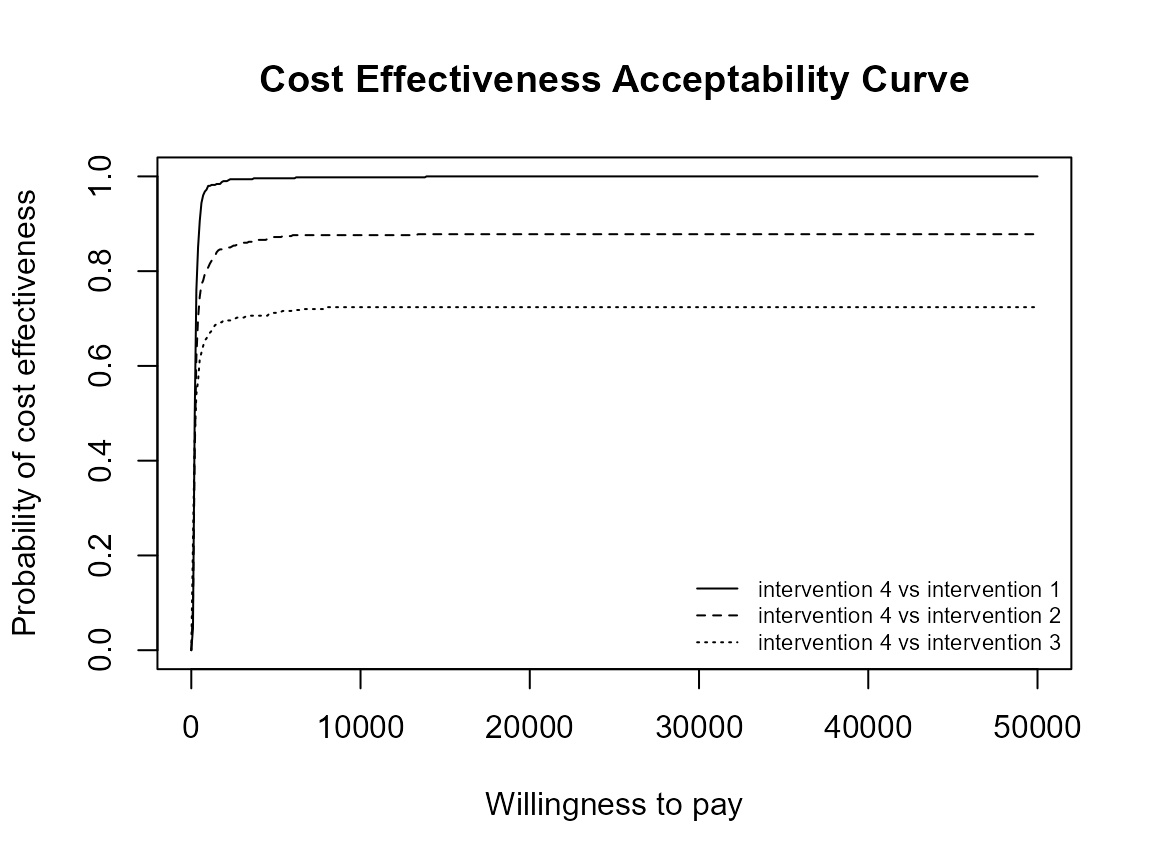
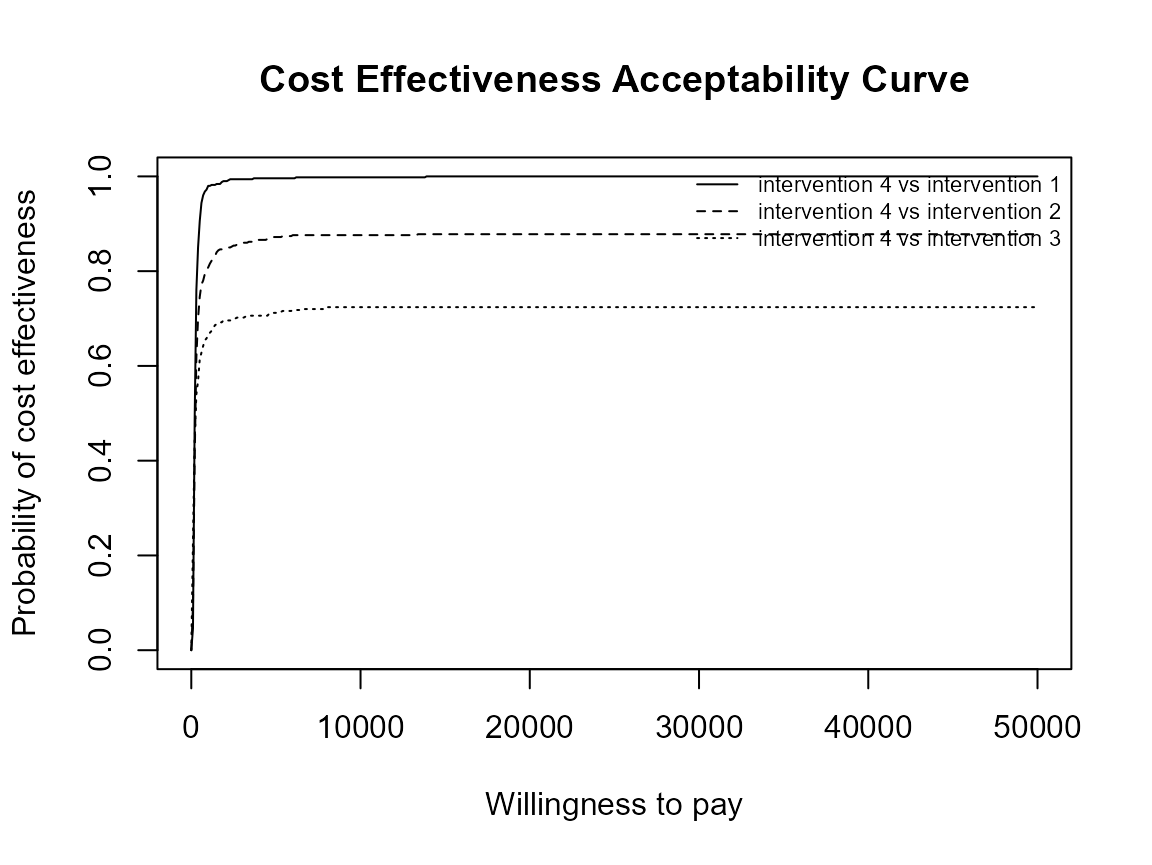
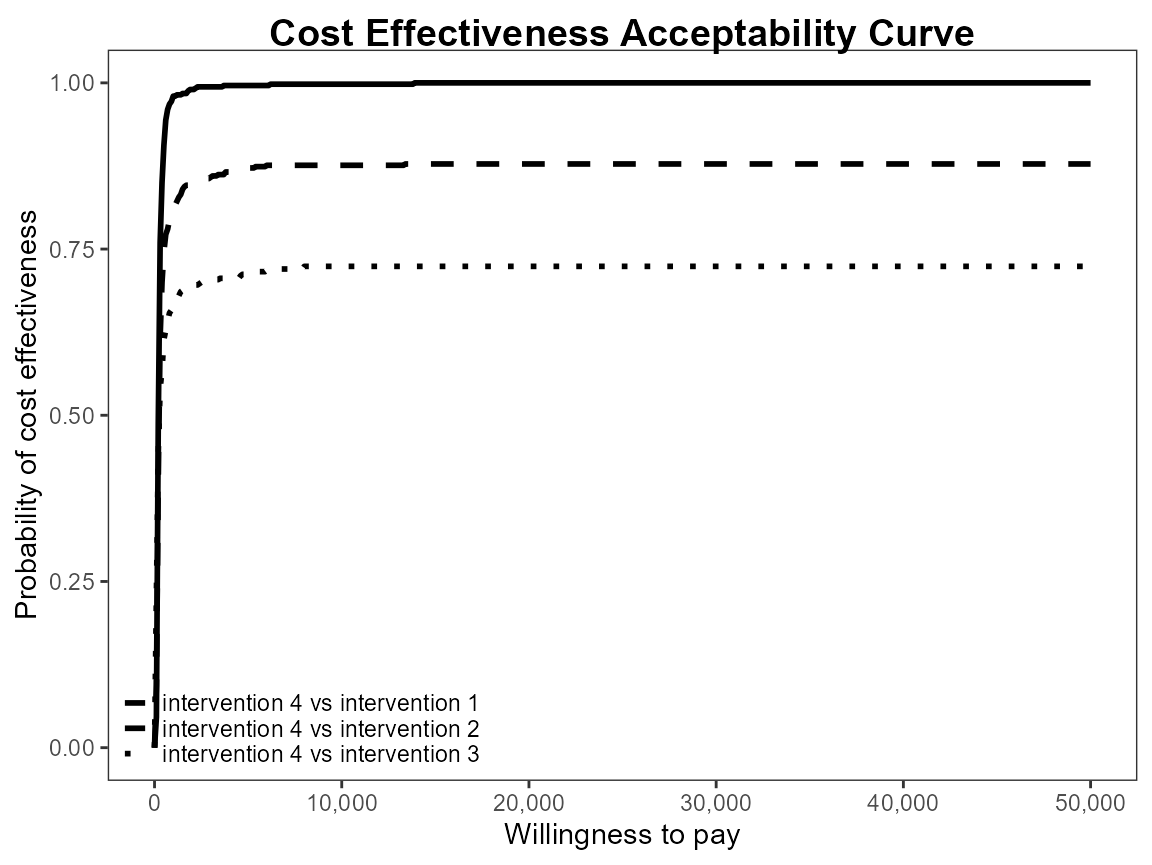
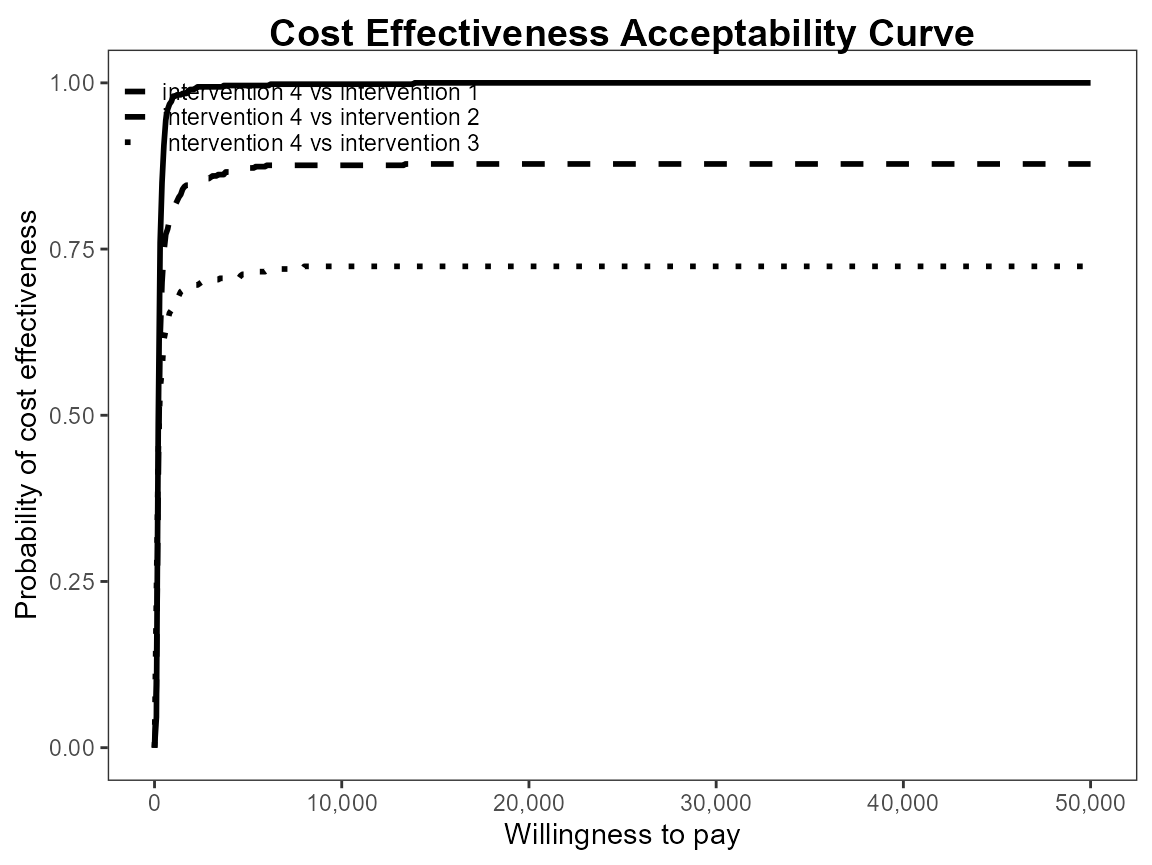
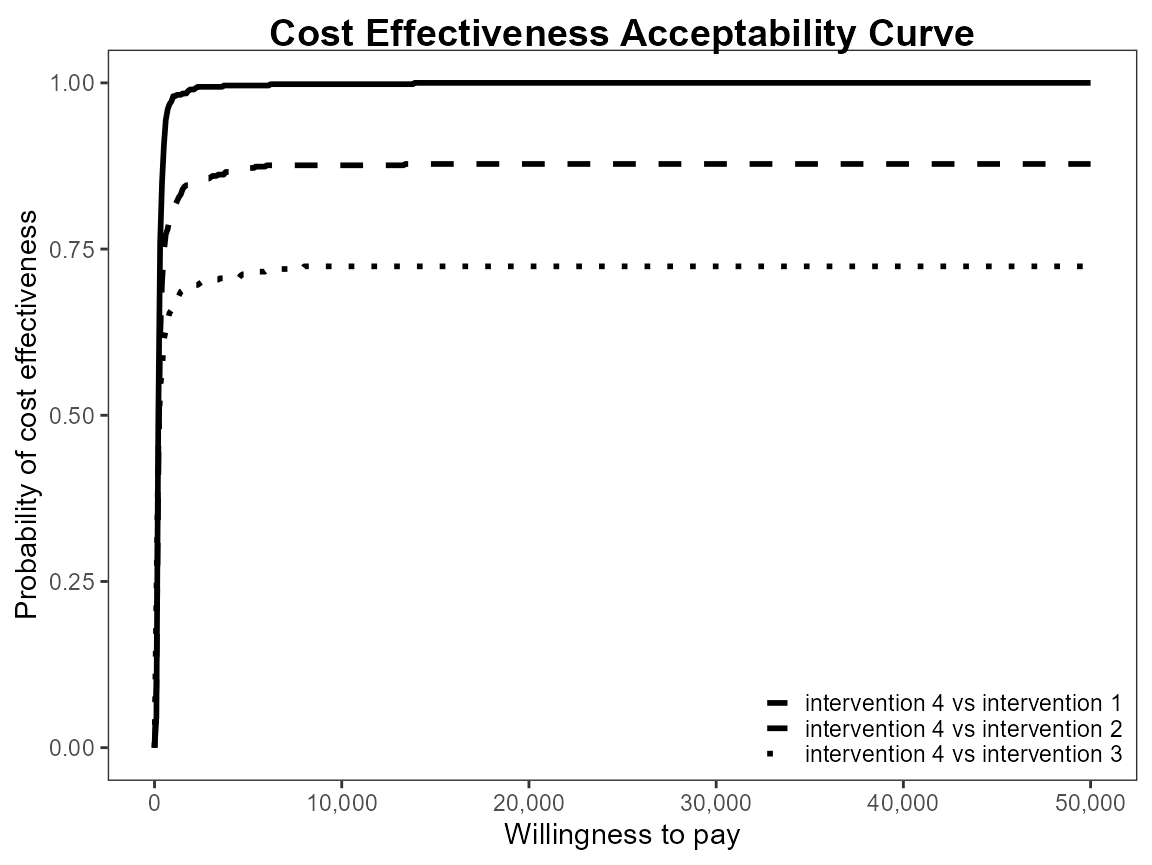
Define colour palette.
mypalette <- RColorBrewer::brewer.pal(3, "Accent")
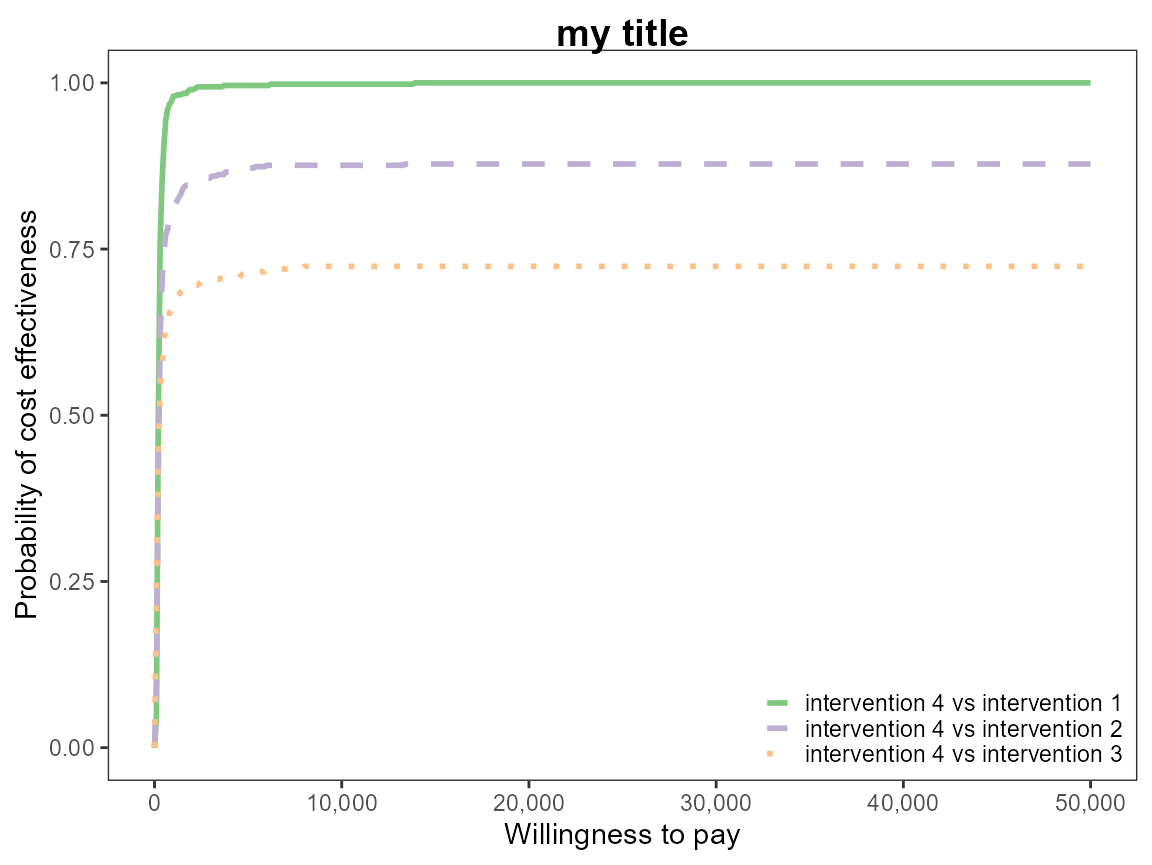
ceac.plot(he,
graph = "base",
title = "my title",
line = list(color = mypalette),
pos = FALSE)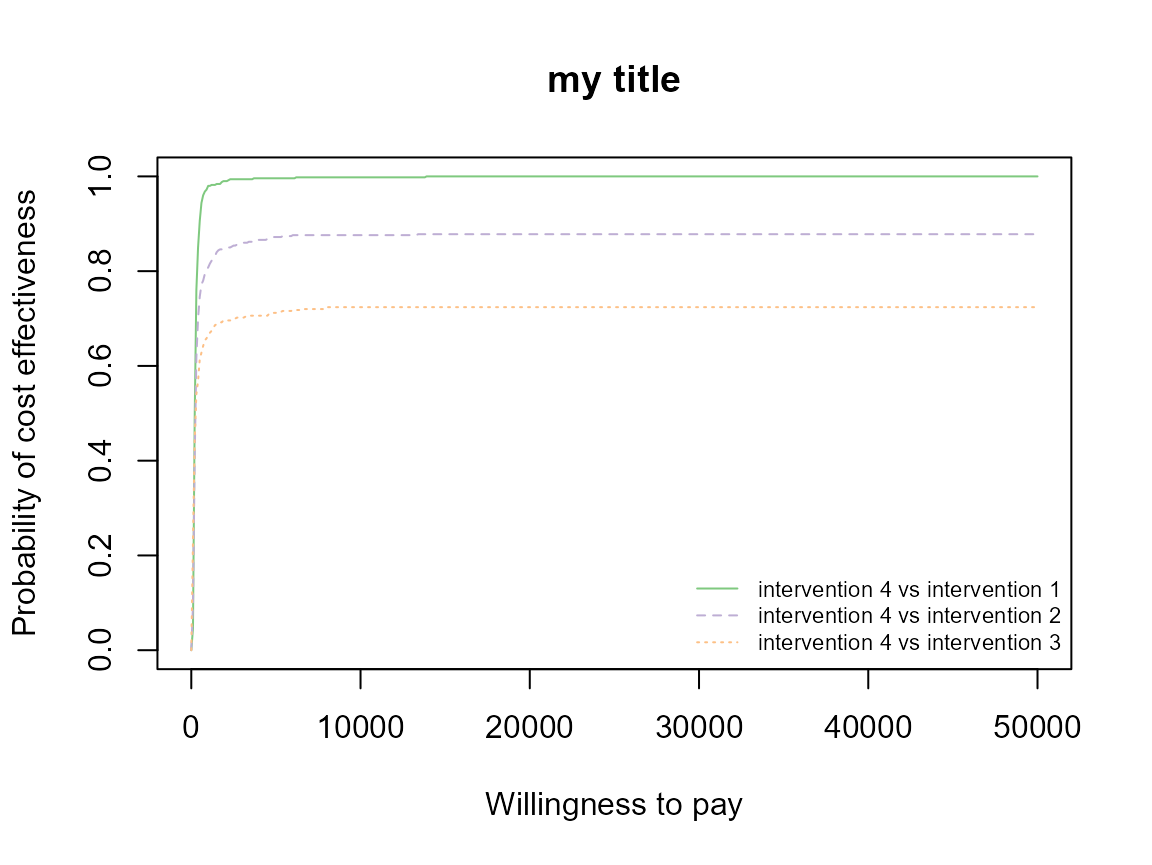
Pair-wise comparisons
Again, without loss of generality, if we assume that we are interested in intervention \(i=1\), then we wish to calculate
\[ p(NB_1 = \max\{NB_i : i \in S\} | k) \]
This can be approximated by the following.
\[ \frac{1}{N} \sum_j^N \prod_{i \in S} \mathbb{I} (k \Delta e_{1,i}^j - \Delta c_{1,i}^j) \]
R code
In BCEA we first we must determine all combinations of paired
interventions using the multi.ce() function.
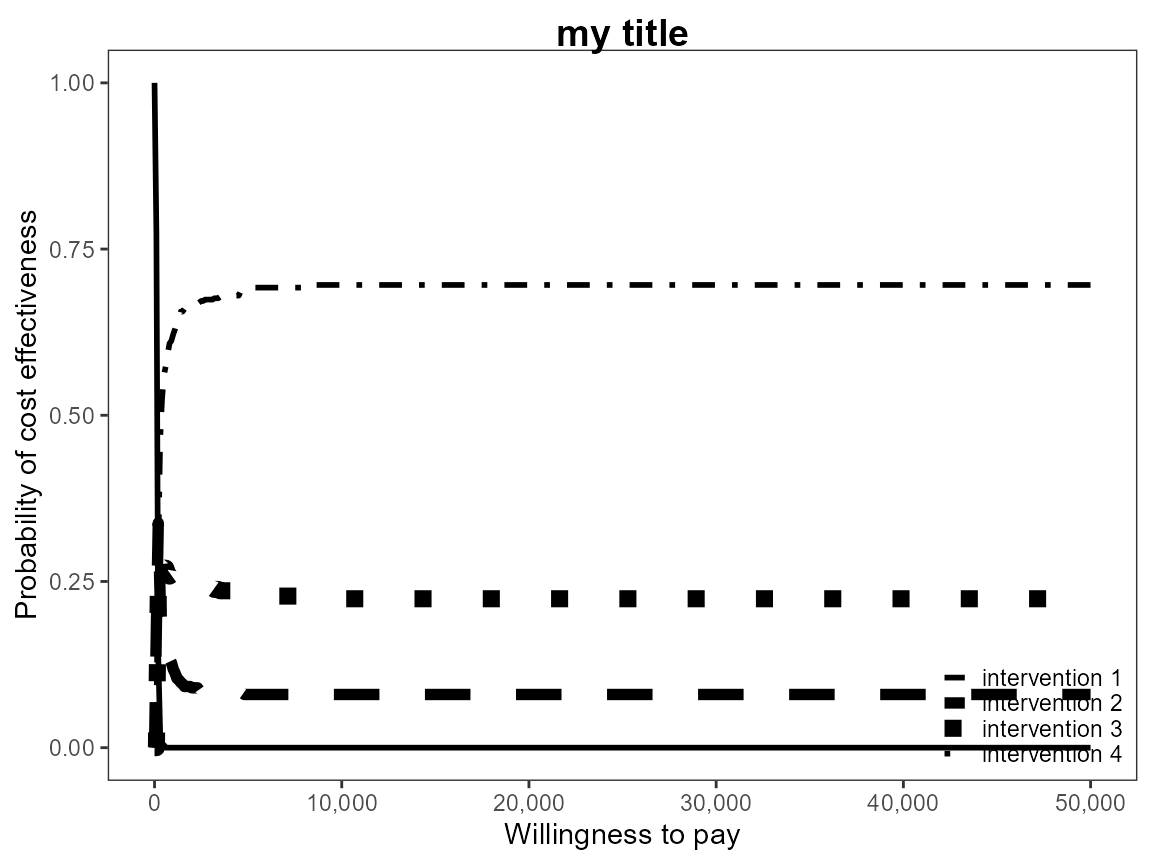
he <- multi.ce(he)We can use the same plotting calls as before
i.e. ceac.plot() and BCEA will deal with the pairwise
situation appropriately. Note that in this case the probabilities at a
given willingness to pay sum to 1.
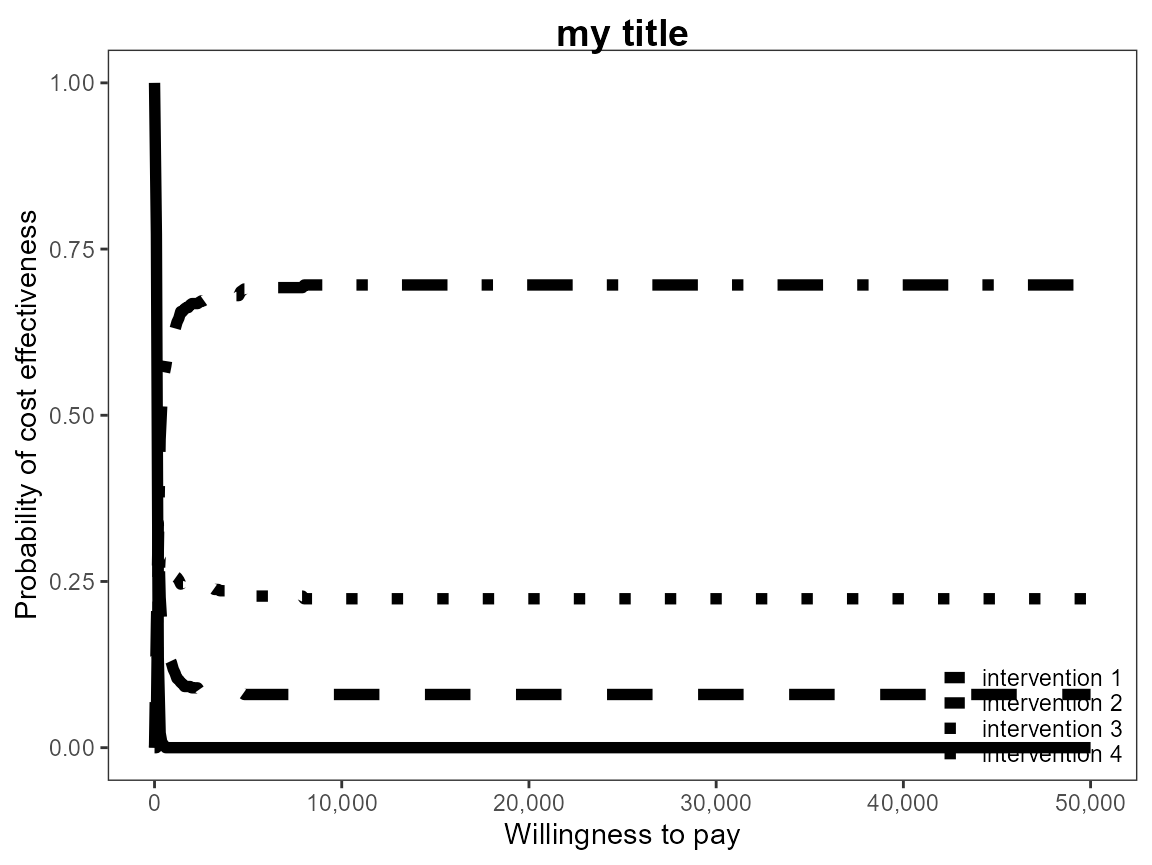
ceac.plot(he, graph = "base")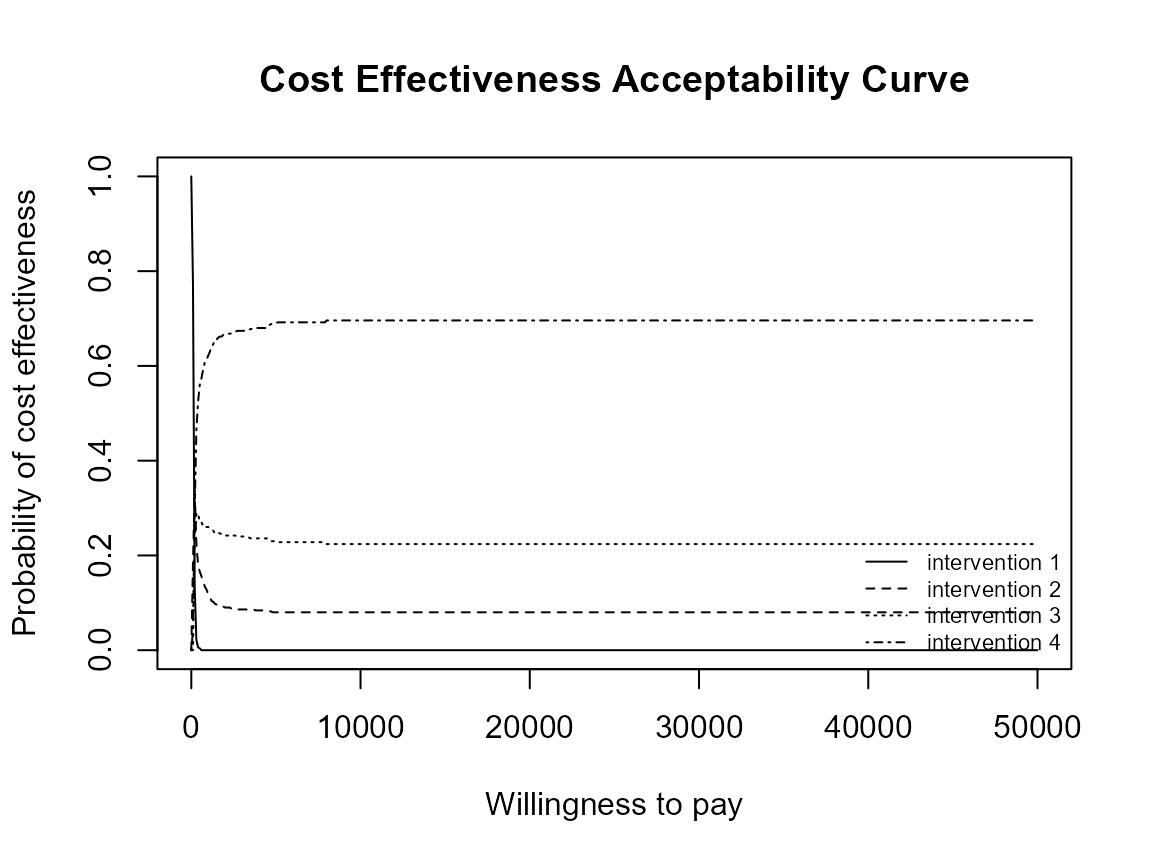
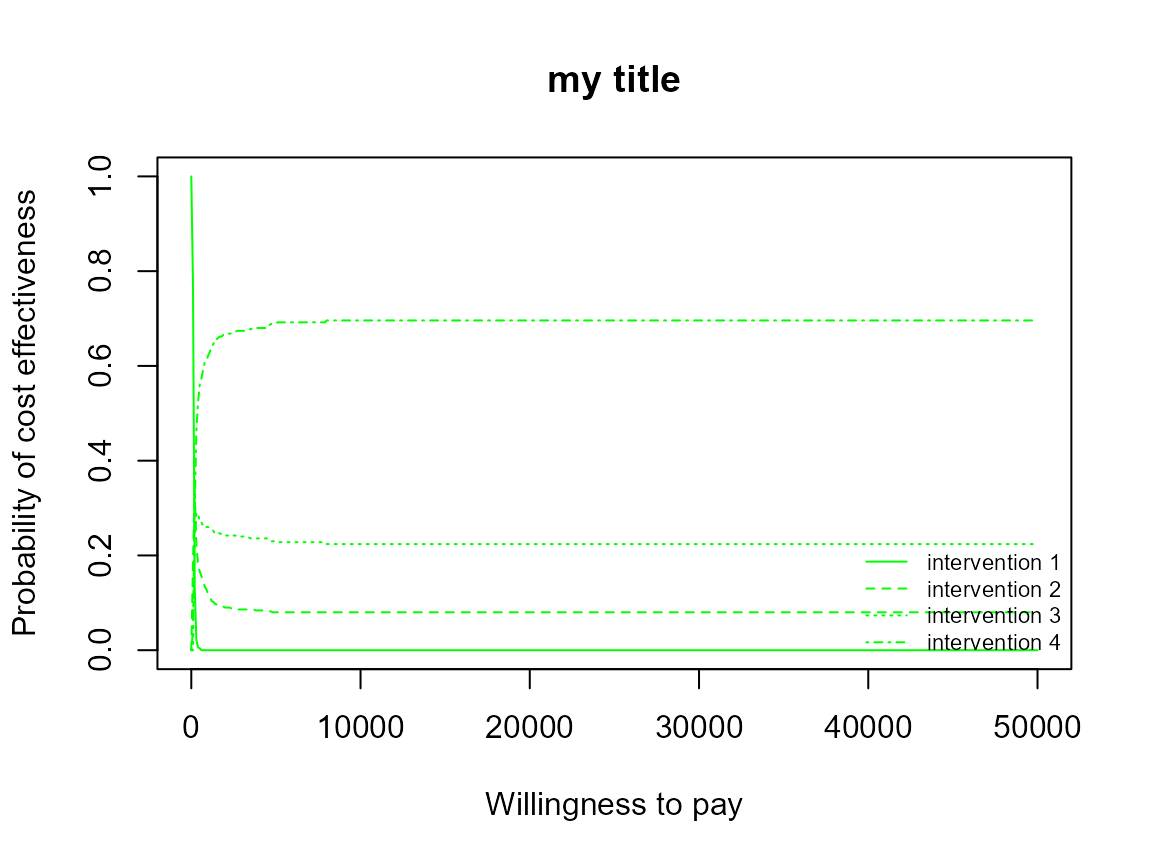
mypalette <- RColorBrewer::brewer.pal(4, "Dark2")
ceac.plot(he,
graph = "base",
title = "my title",
line = list(color = mypalette),
pos = c(0,1))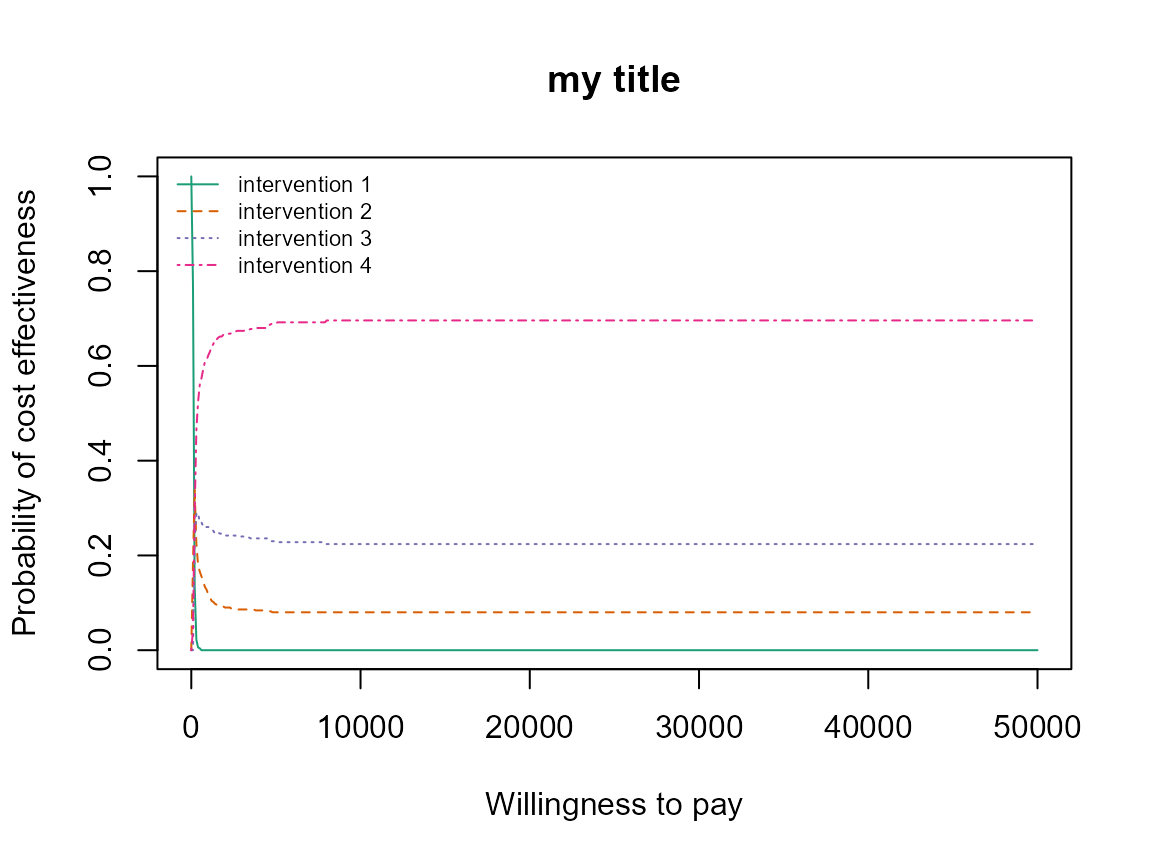
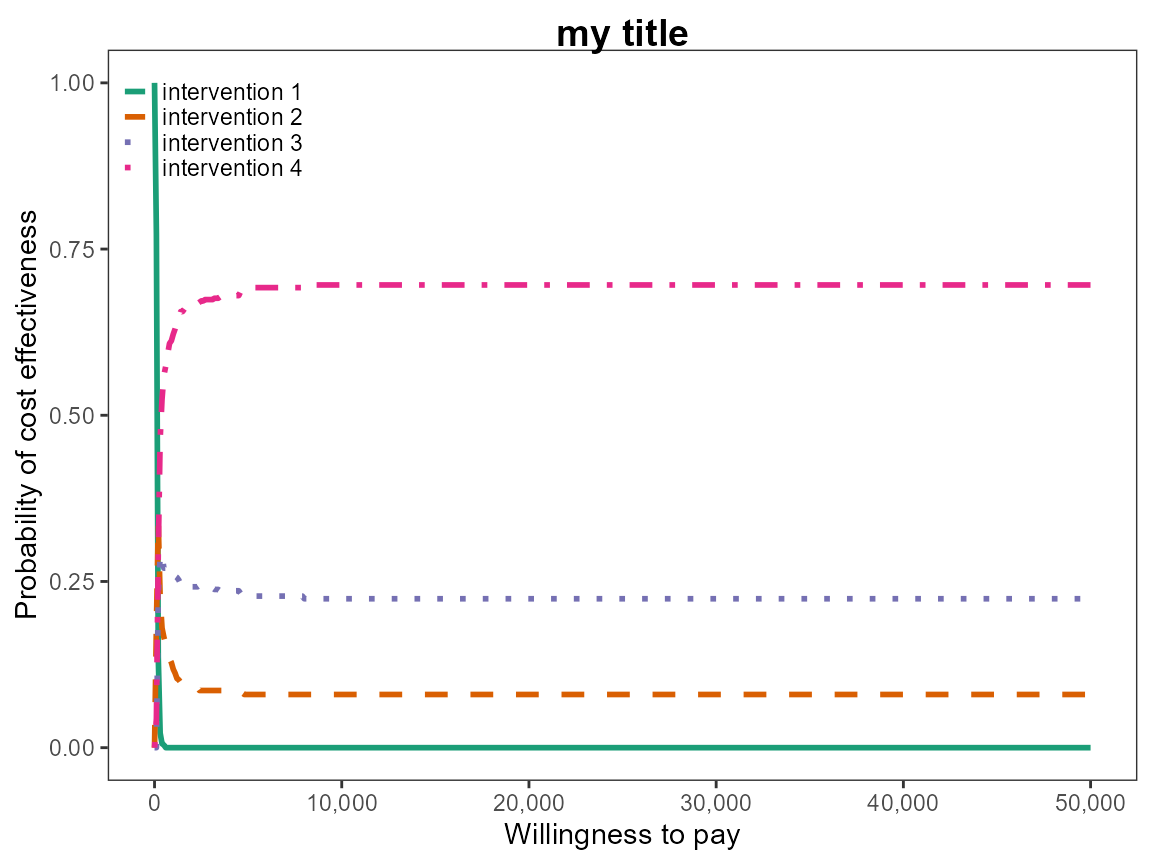
The line width can be changes with either a single value to change all lines to the same thickness or a value for each.